这是一个初中数学教程 - chushu wiki

1 - 本文书写格式

1.1 - 图片

图片应该放在根目录中的“img”文件夹中，标注在那一章引用的图片。
标准的格式应该为："需要插入图片文章的一级标题_这篇文章的第几个图片"

例子

假入本文需要插入第一个图片，图片名称应该叫做"1_1.png"

1.2 - 文章格式

文章需要严格的遵行 Makedown 语法

1.2.1 - 在每个标题之前添加序号。

标准的格式应该为："序号 - 标题"

例子

例：这是本文章的第二点，所以应该是"1.2 - 文章格式"

1.2.2 - 例子和注意应该使用 Material for MkDocs 扩展中的 Admonitions 例子

不得不说，这个插件是真的强大，提供了 Markdown 许多先进的功能本文中使用的例子插件也是其中之一的。最初是在知乎中一个知乎网友发现的。篇幅限制，本文只讲例子和警告的写法，更多的信息请参考Material for MkDocs 官网

例子的标准的书写格式应该为(例子内容前面是[Tab])：

!!!example 例子
    例子内容

注意的标准写法应该是(注意的内容前面是[Tab])：

!!!warning 注意
    注意的内容

例子

这就是一个例子

注意

注意应该这么写

1.2.3 - 文章标明作者名字的首字母

例子

"zjx"

1.2.4 - 文章整体结构

例子

0 - 主标题

0.1 - 二级标题

0.1.1 - 三级标题

正文

作者名称（或者作者名称各个汉字首字母）

1.3 - 数学公式

本文章插入数学公式使用 LaTeX 公式输入

1.3.1 - LaTeX的使用方法

1.3.1.1 - 基本用法

例子

输入"$y = kx+b$"
得到
$y = kx+b$

1.3.1.2 - 可能用到的常用标注

符号	表示方法	符号	表示方法
$\alpha$	\alpha	$\beta$	\beta
$a^2$	a^2	$\pm$	\pm
$\times$	\times	$\div$	\div
<	\lt	>	\gt
$\leq$	\leq	$\geq$	\geq
$\neq$	\neq	$\approx$	\approx
$\angle$	\angle	$10^\circ$	10^\circ
$\perp$	\perp	$\sin$	\sin
$\because$	\because	$\therefore$	\therefore

以上内容无法在github中正常显示,请添加图片来插入符号

1.3.2 - 使用方法

标准的格式为：''这是一段文字，后面是公式 $\sin \angle a$ '

例子

这是一段文字，后面是公式 $\sin \angle a$

zjx

2 - 数学常用软件

2.1 - Geogebra

Geogebra 是一个动态几何软件，提供基本的几何作图软件，功能强大
前往

本教程大部分的图片都是Geogebra中的软甲截图

zjx

2.2 - 微软数学

微软数学是一个方便的计算器，大厂支持的软件，但是目前没有 Windows 版本，我们可以下载安卓版本的软件，支持扫描计算，绘图计算和手动输入计算。

电脑可以使用此应用的网页版本，单击下面的链接来打开
打开

zjx

4 - 几何

4.1 - 立体图形

由于这里知识点难点就是正方体，所以这里只讲解正方体

4.1.1 - 正方体

4.1.1.1 - 平面展开图

正方体的平面展开图可以分成 4 类，分别是：
141型，231型，222型，33型
{141型图片}
这是141型的正方体的平面展开图
{231型图片}
这是231型的正方体的平面展开图
{222型图片}
这是222型的正方体的平面展开图
{33型图片}
这是33型的正方体的平面展开图

4.1.1.2 - 找对面

找对面很多人用着很抽象的还原方法，其实并没有这么复杂，我们只需要遵循着一个比较好用的方法：
小马过河

例子

在下面的平面展开图中，标注着 1~6 的数字，请问 2 对面的数字是什么？
{这里应该有一张图片}

首先，我们应该让 2 在岸边，画出一条河流
{这里应该有一张照片}

如果你的河流画的正确且图也是正确的，那么在 2 的对面应该只有一个数字和 2 对应了，这个数字就是 2 对面的那个数字

小技巧

这个方法也可以用来验证这个是否是正确的正方体平面展开图，如果小马过河之后没有陆地，那么这个图形就是不正确的，如下图所示
{这里应该有一张图片}
{这里应该还有一张图片}

这一章节目前没有什么重要的知识点了，如果作者在做题的过程中发现了比较重要的知识点，会及时更新。

zjx

4.2 - 点和线

4.2.1 - 点

在平面上，一个大小可以被忽略的一个物体，可以叫做点。
{点A图片}

4.2.2 - 线

4.2.2.1 - 线段

线段是由无数个点组成的，它有着一个基本事实：

两点之间线段最短

{这里应该有一张图片，线段AB}
上图应该叫做线段AB，又叫做AB两点之间的距离

4.2.2.2 - 射线

让线段的一个端点向远处无限延长的线就叫做射线。
{射线OA 图片}

4.2.2.3 - 直线

让线段的两个端点向远处无限延长的线就叫做直线，它有着一个基本的事实：

两点确定一条直线

{直线图片}

这个直线有着两种叫法，第一种是直线AB，第二种是直线l

zjx

4.3 - 线的位置关系

4.3.1 - 相交

两条直线，在最后的时候会形成一个交点就是相交
{这里有一张迟到的图片}

4.3.1.1 - 对顶角

在两条线相交的时候，会形成四个角，如下图所示的 ∠1 和 ∠2 就是一对对顶角
{这里有一张迟到的图片}
对顶角在题目中最普遍的用法就是下面这个定理
对顶角相等

例子

在下面这张图中， $l1$ 和 $l2$ 相交，一共有两对对顶角，有 ∠1 = ∠3，∠2 = ∠4。
{这里应该有一张迟到的照片}

4.3.1.2 - 垂直

如果两线相交的时候有一个角为 90° 那么就说这两条线垂直。

例子

在如下图所示中，AB 和 CD 互相垂直。
{这里有一张迟到的照片}
AB 和 CD 互相垂直，可以记作 AB ⊥ CD，点 O 叫做垂足。AB 是 CD 的垂线，同时，CD 也是 AB 的垂线

zjx

5 - 函数

5.1 - 函数的定义

5.1.1 - 变量

定义

在研究问题中可以取不同数值的量叫做变量

如果在一个变化过程中有两个变量，例如 $x$ 和 $y$ ，对于 $x$ 取到了一个值， $y$ 只有唯一的值和它对应。因此 $x$ 叫做自变量，意思是“自己变化的量”；而 $y$ 就叫做因变量，意思是“因为自变量变化的量”

例子

在 $y = 2x + 3$ 中的 $x$ 叫做自变量， $y$ 叫做因变量
在 $S = \pi r^2$ 中的 $r$ 叫做自变量， $S$ 叫做因变量

注意

自变量的取值范围应该符合实际的意义`

例

在上面的第二个例子中，自变量 $r$ 表示圆的半径，要取值都是正实数.

5.1.2 - 常量

定义

在研究问题中取值一直不变的量叫做常量

例子

在上面的第一个例子中，2和3是常量
在上面的第二个例子总， $\pi$ 是常量

5.1.3 - 平面直角坐标系

定义

两条数轴，原点重合，互相垂直，且具有相同单位长度，这样就建立了一个平面直角坐标系。
两条数轴分别取向上和向右为正方向
两条数轴的交点 $O$ 叫做坐标原点。
从右上角开始逆时针分别是第一象限，第二象限，第三象限，第四象限

在平面直角坐标系上表示一个点

例子

A (3, 4)
A的图片

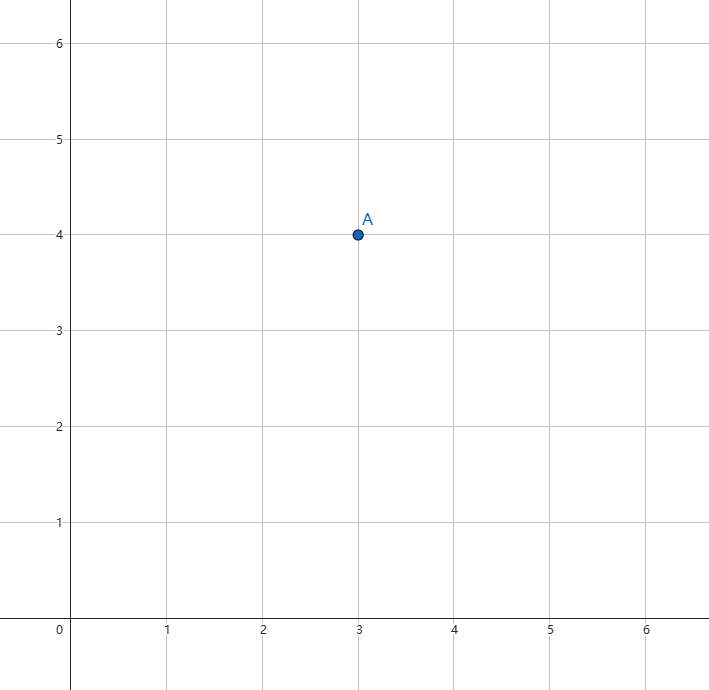
这样就可以在坐标系内表示一个点了。
3，也就是括号里的第一项，代表着横坐标，也就是点到 $y$ 轴的距离
4，也就是括号内的第二项，代表着纵坐标，也就是点到 $x$ 轴的距离

这样，我们就可以成功的在坐标轴内表示一个点了

在平面直角坐标系中表示一个函数图像

在平面直角坐标系内表示一个函数图像分为三步：
1.列表
2.描点
3.连线

画出 $y = x + 4$ 的图像

1.列表

x	-2	-1	0	1	2
y	2	3	4	5	6

2.描点
描点图片
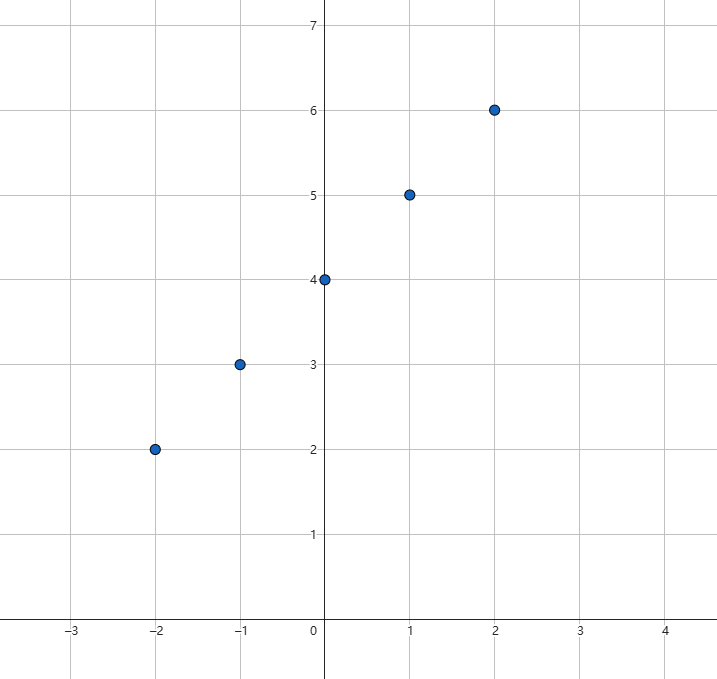
3.连线
连线图片

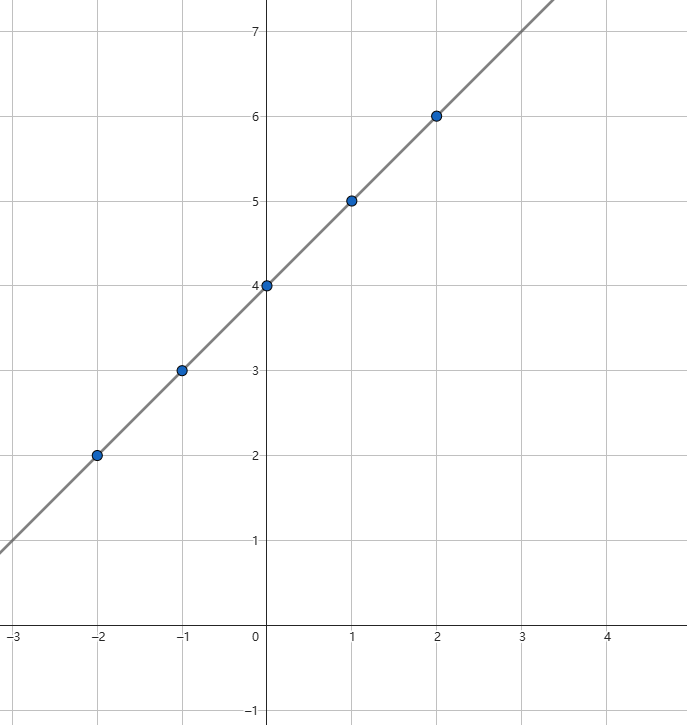
这样，我们就成功的完成了函数图像的绘制

注意

每一个 $x$ 的值只能对应一个 $y$ 值，也就是说，在平行于 $y$ 轴的一条直线上，不能经过函数图像两次

zjx

5.2 - 正比例函数

5.2.1 - 图像

正比例函数的图像就是一条经过原点的直线
tupian

5.2.2 - 函数关系式

正比例函数的函数关系式为：

$y = kx$

其中， $y$ 和 $x$ 是变量
$k$ 是一个常量，它的名称叫做斜率，决定着这一条直线的倾斜程度。 $k$ 的值越大，这条直线与 $x$ 轴的夹角越大，也就是越靠近 $y$ 轴

那么， $k$ 的正负对函数又有什么影响呢？

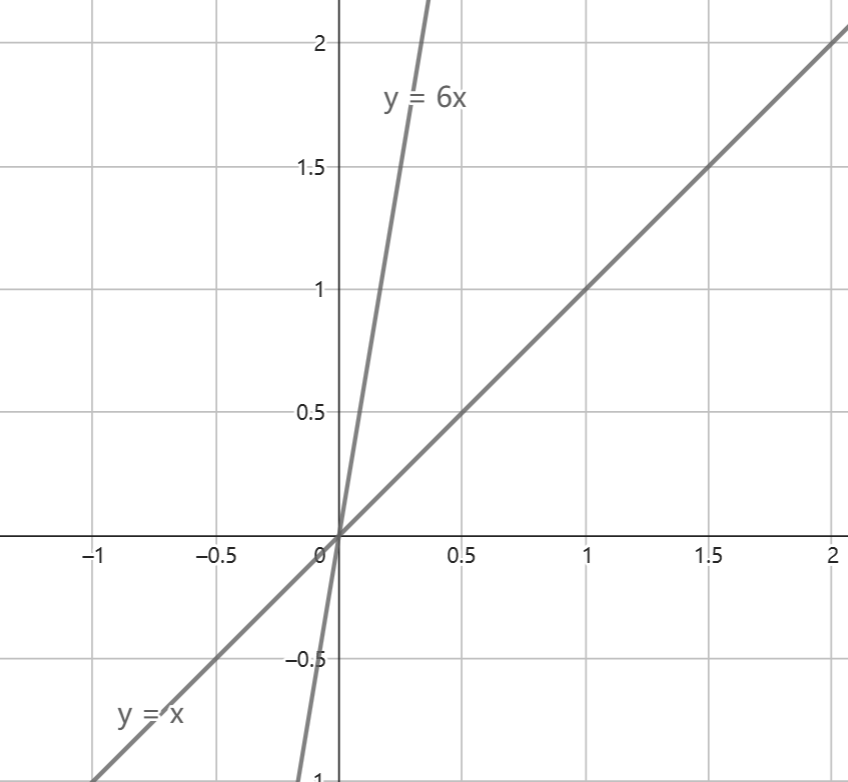
例子

下面是 $y = 2x$ 和 $y = -2x$ ，的函数图像
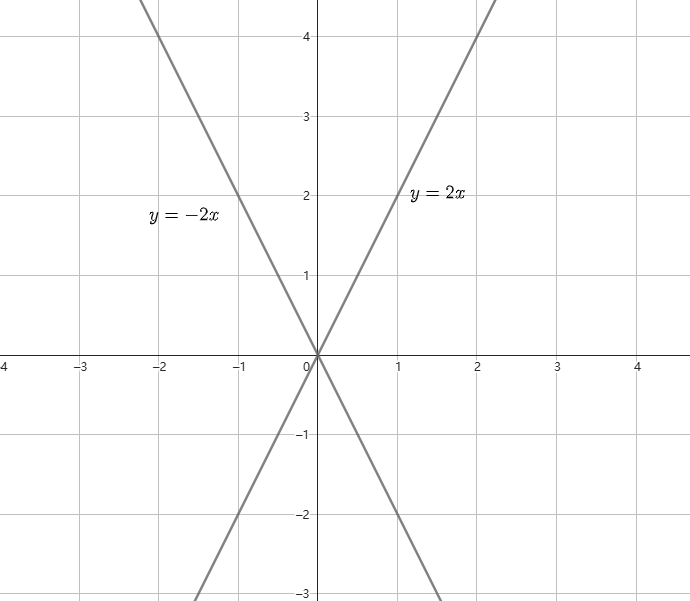
tupian2

由此我们可以看出
当 k > 0 时， $y$ 随 $x$ 的增大而增大，
当 k < 0 时， $y$ 随 $x$ 的增大而减小。

注意

$k$ 的值是不能为 0 的，因为 $k$ 的值如果为 0 ，函数关系式就变成了 $y = 0$ 自变量就消失了，因此它就不是一个函数了...

注意

正比例函数 $k$ 越大，会越接近于 $y$ 轴，但是正比例函数永远无法和 $y$ 轴重合

zjx

5.3 - 一次函数

5.3.1 - 图像

一次函数的图像是一条直线，但是这次，只要是函数的直线，就是一次函数

注意

既然一次函数是一个函数了，那么这条直线就不能平行于 $x$ 轴或 $y$ 轴

当然正比例函数就是特殊的一次函数，下面的图片是几个一次函数图像。
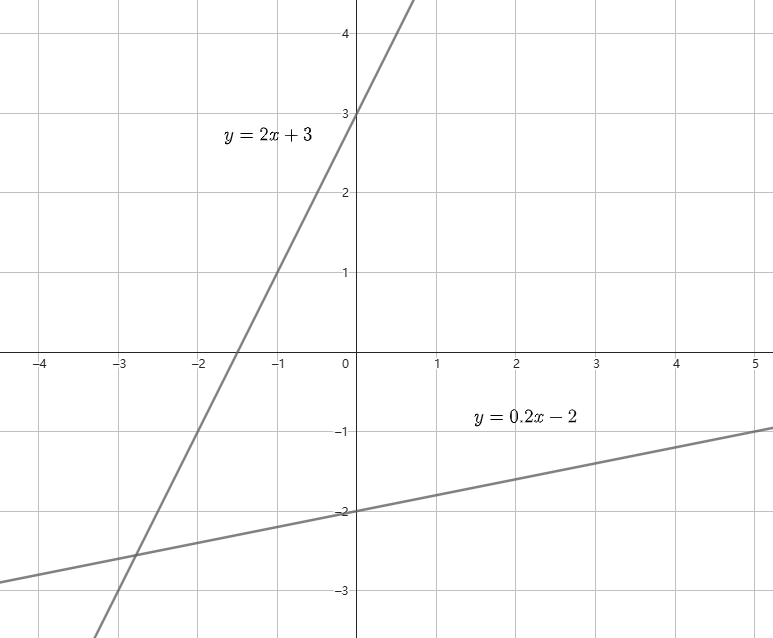
tupian1

5.3.2 - 函数关系式

一次函数的函数关系式是

$y = kx + b$

可以看出它的函数关系式和正比例函数的函数解析式多了一个 $b$ 这个 $b$ 到底是决定了什么呢，我们可以通过下面的图像来探究一下

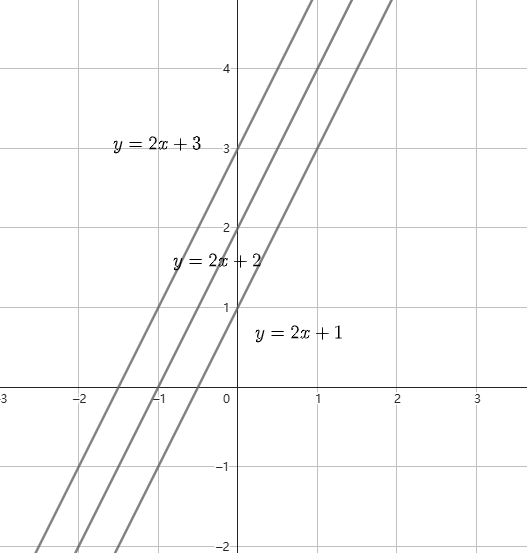
tupian2

由上面的图片可以看出， $b$ 的值决定了直线于 $y$ 轴的交点位置

例子

在 $y = 2x +4$ 中，这个图像与 $y$ 轴的交点为 $(0,4)$
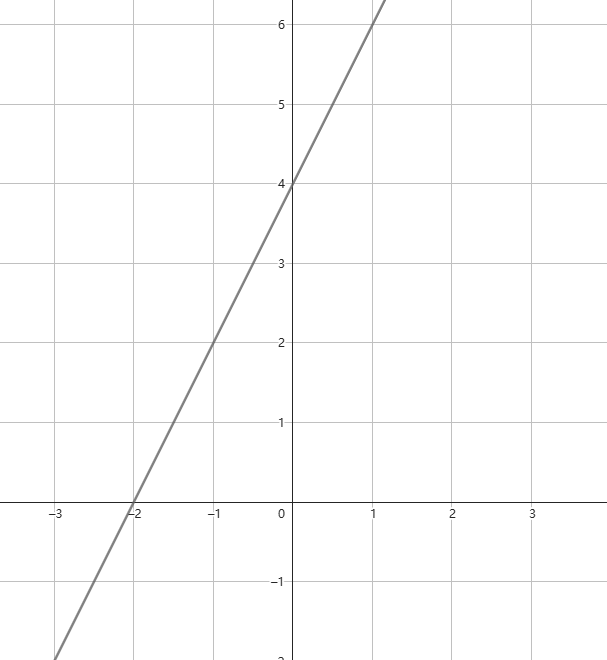
tupian3

5.3.3 - 求一次函数的函数解析式

前面我们提到过，两点确定一条直线，也就是说，一次函数，也可以用两个点来确定
常用的方法叫做待定系数法

现在，有一个一次函数的图像经过 $(c,d)$ 和 $(e,f)$ ，那么这个一次函数的函数解析式是什么？

设 $y = kx + b$
将 $(a,b)$ 和 $(c,d)$ ，带入，得
$\begin{cases} d = ck + b \\ f = ek + b \end{cases}$
解的 $\begin{cases} k = g \\ b = l \end{cases}$
$\therefore y = gx + l$

注意

这里的 $c,d,e,f,g,l$ 均为一个常数

5.2.4 - 其他直线

上文中提到，是函数的直线才是一次函数，但是不是函数的直线我们应该怎么表示呢？

5.2.4.1 - 平行于 $x$ 轴的直线

平行于 $x$ 轴的直线可以使用下面的式子来表示：

$y = a$

其中， $a$ 代表着一个常量。也就式说，在这条直线上的任意一点，纵坐标都为 $a$

例子

$y = 4$ 的图像如下图所示
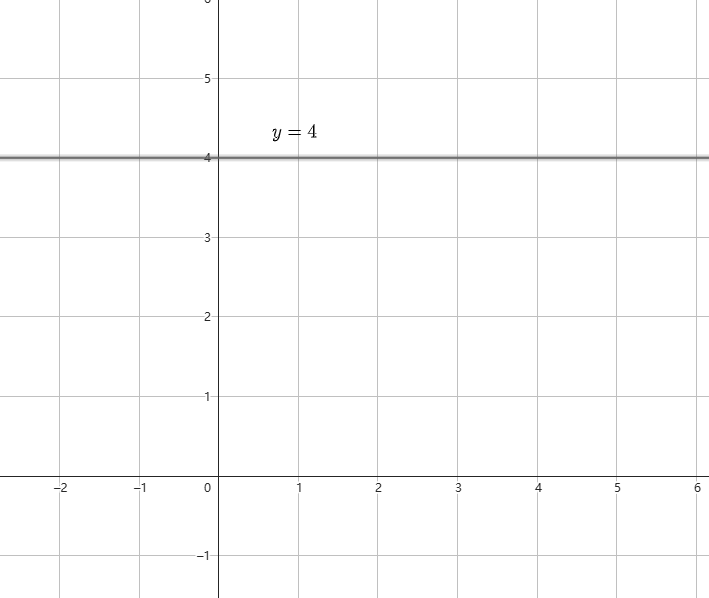
tupian3

5.2.4.2 - 平行于 $y$ 轴的直线

平行于 $y$ 轴的直线可以使用下面的式子来表示

$x = a$

其中， $a$ 代表着一个常量，也就是说，在这条直线上的任意一点，横坐标都为 $a$

zjx

5.4 - 反比例函数

5.4.1 - 图像

反比例函数的图像就不是很好解释了，它又叫做双曲线，它的图像是由两条在奇数象限（一三象限）或者偶数象限（二四象限）的曲线组成的。下面是反比例函数图像 $y = \frac{1}{x}$ 的图像
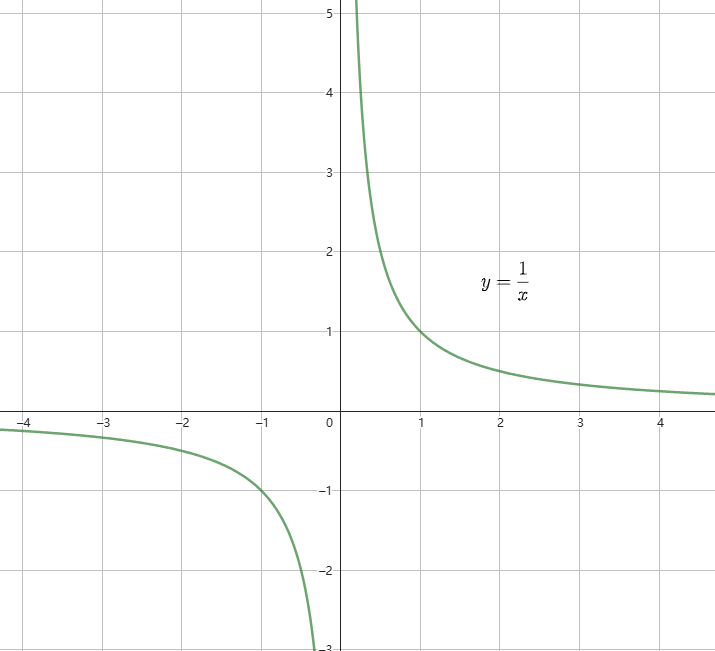
tupian1

5.4.2 - 函数解析式

反比例函数的函数解析式为：

$y = \frac{k}{x}$

其中， $k$ 是一个常量，那么这个常量决定的是什么呢？

我们可以先在函数图像上找到一个点
然后向 $x$ 轴和 $y$ 轴作垂线，这样反比例函数就和两条轴形成了一个矩形。
经过计算发现，这个矩形的面积永远不变，且它的面积的值就是 $k$ 。

例子

在函数解析式 $y = \frac{12}{x}$ 与两轴的垂线形成的矩形的面积就为 $12$ .
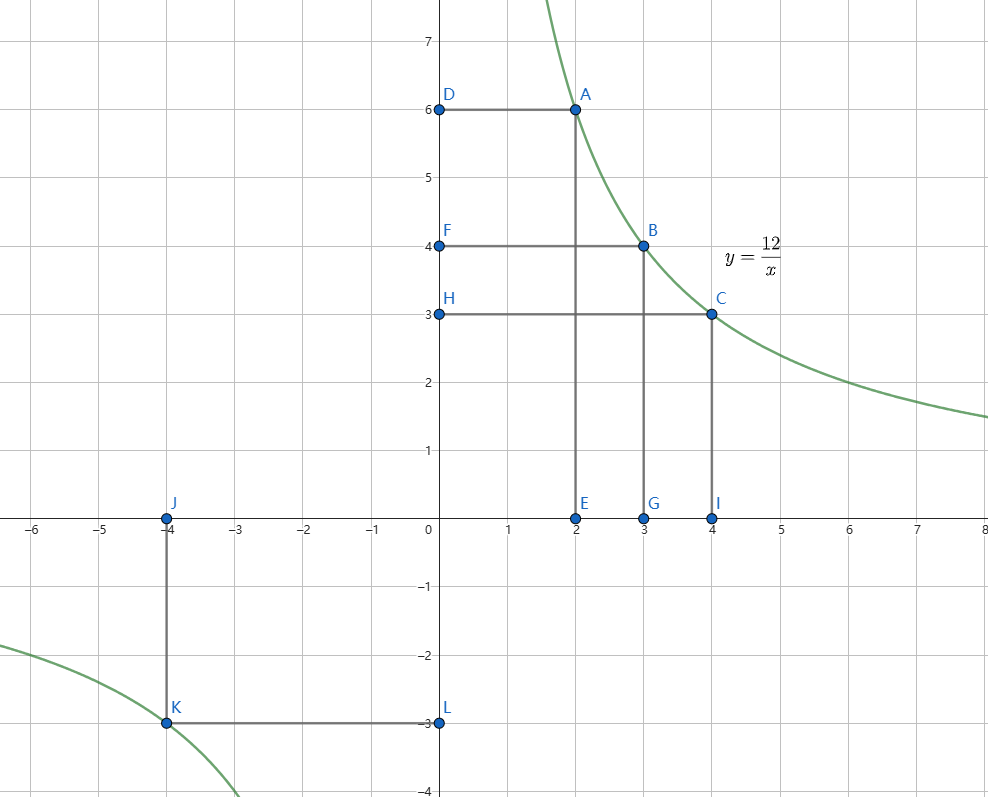
tupai2

相信你也猜到了， $k$ 的正负肯定也影响图像。那么， $k$ 的正负对图像的影响是是怎样的呢？

例子

下面是 $y = \frac{12}{x}$ 和 $y = \frac{-12}{x}$ 的图像
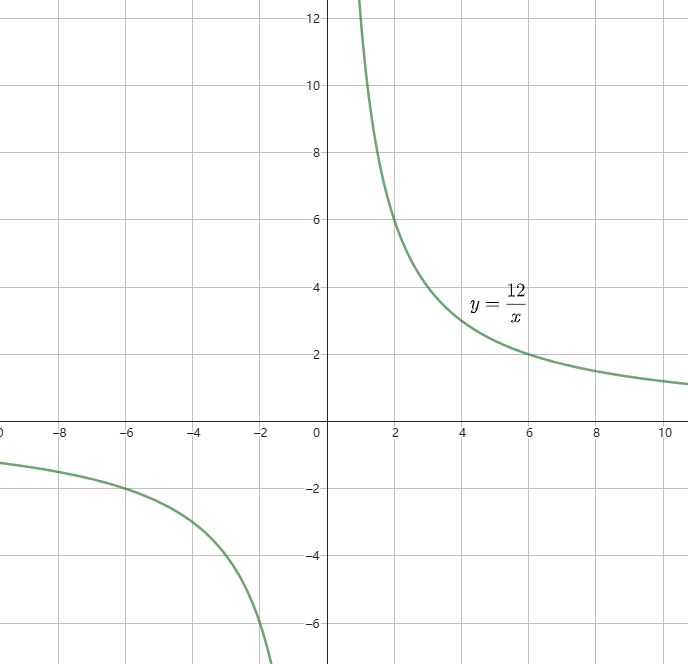
tupain3
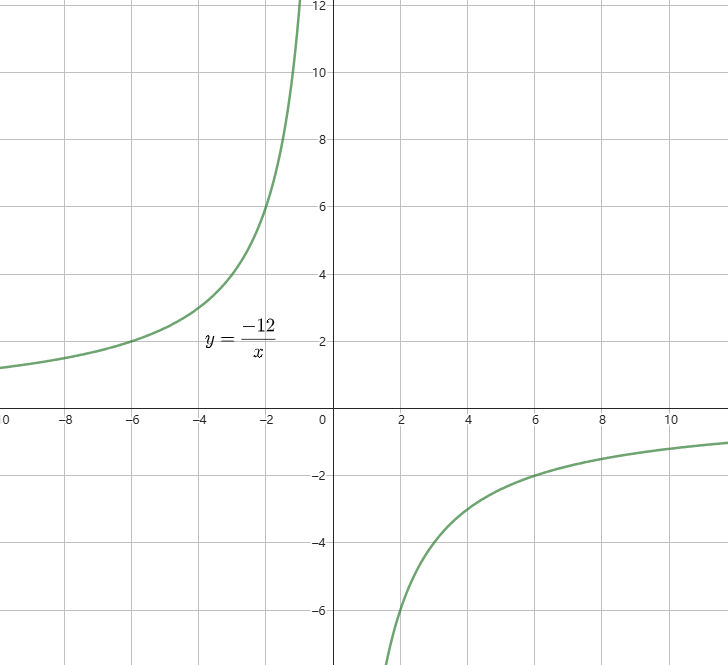
tupian4

我们可以看到
当 k > 0 时， $y$ 随 $x$ 的增大而减小，且图像在一三象限上
当 k < 0 时， $y$ 随 $x$ 的增大而增大，且图像在二四象限上

5.4.3 - 函数解析式求法

求法和一次函数是一样的，也是使用待定系数法

一个反比例函数经过点 $(a, b)$ ，那么这个反比例函数的函数解析式是什么？

解：设 $y = \frac{k}{x}$
将 $(a, b)$ 带入，得
$b = \frac{k}{a}$
解的 $k = ab$

zjx

5.5 - 二次函数

5.5.1 - 图像

二次函数的图像是一条抛物线，它是一条曲线下面是二次函数 $y = x^2$ 的图像
{这里有一张迟到的照片~}

5.5.2 - 函数解析式

二次函数的函数解析式有三个

5.5.2.1 - 一般式

$y = ax^2 + bx + c$

这里的 $b$ 自己是什么都都不决定的，但是后面会说，那么 $a$ 和 $c$ 决定着什么呢？

例子

观察下面的 $y = 3x^2$ ， $y = 2x^2$ 和 $y = -3x^2$ 的图像
{这里有一张迟到的照片~}

从上面的例子我们可以看出， $a$ 决定着抛物线开口大小和方向

$a$ 的值越大，抛物线就越靠近 $y$ 轴
当 a < 0 的时候，抛物线开口向下
当 a > 0 的时候，抛物线开口向上

注意

$a \neq 0$ ，否则，二次函数的二次项就会消失，那它还是二次函数吗？

例子

观察下面的 $y = 3x^2 + 1$ ， $y = 3x^2 + 2$ 和 $y = 3x^2 + 3$ 的图像
{这里有一张迟到的照片~}

从上面的例子可以看出， $c$ 决定着抛物线与 $y$ 轴的交点

5.5.2.2 - 顶点式

$y = a(x - h)^2 + k$

有人可能会疑惑，二次函数的顶点是什么呢？观察图象我们可以看出来，二次函数总是有一个最高点或者最低点，这就是二次函数的顶点

这是二次函数的顶点式，这是由二次函数最基本的 $y = x^2$ 平移得出的，任何图像的平移都遵循左加右减，上加下减，这样它的顶点是 $(h, k)$

顶点坐标的推导过程

相信你一定在代数部分已经学习过配方法解决一元二次方程了，下面是具体的解决步骤

1.提取公因式

$y = a(x^2 + \frac{b}{a}x) + c$

2.配方

$y = a(x^2 + \frac{b}{a}x + \frac{b^2}{4a^2})-\frac{b^2}{4a}+c$

3.化简

$y = a(x^2 + \frac{b}{2a})+\frac{4ac - b^2}{4a}$

由此可见， $h = -\frac{b}{2a}$ ， $k = \frac{4ac - b^2}{4a}$ ，通过这个式子，我们就可以得出顶点坐标的求法了，这在24题中显得尤为重要

这样就可以解释了，既然抛物线的对称轴为 $-\frac{b}{2a}$ ，那么当 $a$ ， $b$ 同号的时候，对称轴为负，那么抛物线对称轴在 $x$ 轴的负半轴上，反之当 $a$ ， $b$ 异号的时候，对称轴为正，那么抛物线对称轴在 $x$ 轴的正半轴半轴上，这个现象可以简记为左同右异

5.5.2.3 - 双根式

$y=a(x-x_1)(x-x_2)$

这是二次函数的双根式， $x_1$ ， $x_2$ 分别是抛物线与 $x$ 轴的交点横坐标。非考点，因此在这里不在过多赘述

5.5.3 - 二次函数解析式的求法

二次函数的解析式求法同样遵循着待定系数法，我们可以利用它来求取，但是使用不同的函数解析式，需要带入的数值不同

1.一般式需要带入三个不相同点的坐标，求出 $a, b, c$
2.顶点式需要带入顶点坐标，之后再带入一个其他的点，求出 $a$ ，并且将顶点也带入 $h, k$ 中
3.双根式需要带入抛物线与 $x$ 轴的两个交点，并且再带入一个其他点求解 $a$ ，并将抛物线与 $x$ 轴的两个交点带入解析式

5.5.4 - 一元二次不等式

运用二次函数，我们可以解决一元二次不等式的问题。

首先，我们拿到了一个不等式，看见它含有二次项，我们就可以考虑用二次函数来解决了。
前面我们提到了，二次函数是有顶点的的，而二次函数的开口决定了是取顶点的上面还是下面的部分。

如果 a > 0，不等式解集取顶点上方
如果 a < 0，不等式解集取顶点下方

zjx

这是一个初中数学教程 - chushu wiki

1 - 本文书写格式

1.1 - 图片

1.2 - 文章格式

1.2.1 - 在每个标题之前添加序号。

1.2.2 - 例子和注意应该使用 Material for MkDocs 扩展中的 Admonitions 例子

1.2.3 - 文章标明作者名字的首字母

1.2.4 - 文章整体结构

0 - 主标题

0.1 - 二级标题

0.1.1 - 三级标题

1.3 - 数学公式

1.3.1 - LaTeX的使用方法

1.3.1.1 - 基本用法

1.3.1.2 - 可能用到的常用标注

1.3.2 - 使用方法

2 - 数学常用软件

2.1 - Geogebra

2.2 - 微软数学

4 - 几何

4.1 - 立体图形

4.1.1 - 正方体

4.1.1.1 - 平面展开图

4.1.1.2 - 找对面

4.2 - 点和线

4.2.1 - 点

4.2.2 - 线

4.2.2.1 - 线段

4.2.2.2 - 射线

4.2.2.3 - 直线

4.3 - 线的位置关系

4.3.1 - 相交

4.3.1.1 - 对顶角

4.3.1.2 - 垂直

5 - 函数

5.1 - 函数的定义

5.1.1 - 变量

定义

5.1.2 - 常量

定义

5.1.3 - 平面直角坐标系

定义

在平面直角坐标系上表示一个点

在平面直角坐标系中表示一个函数图像

5.2 - 正比例函数

5.2.1 - 图像

5.2.2 - 函数关系式

5.3 - 一次函数

5.3.1 - 图像

5.3.2 - 函数关系式

5.3.3 - 求一次函数的函数解析式

5.2.4 - 其他直线

5.2.4.1 - 平行于 轴的直线

5.2.4.2 - 平行于 轴的直线

5.4 - 反比例函数

5.4.1 - 图像

5.4.2 - 函数解析式

5.4.3 - 函数解析式求法

5.5 - 二次函数

5.5.1 - 图像

5.5.2 - 函数解析式

5.5.2.1 - 一般式

5.5.2.2 - 顶点式

5.5.2.3 - 双根式

5.5.3 - 二次函数解析式的求法

5.5.4 - 一元二次不等式

5.2.4.1 - 平行于 $x$ 轴的直线

5.2.4.2 - 平行于 $y$ 轴的直线